Logistic Regression

참(1)과 거짓(0) 사이를 구분하는 Regression.

확률 값을 예측하기에 Regression이지만, 그 목적은 Classification에 있다.
어떠한 threshold보다 regression 값이 작거나 큼에 따라 1 혹은 0으로 분류한다.

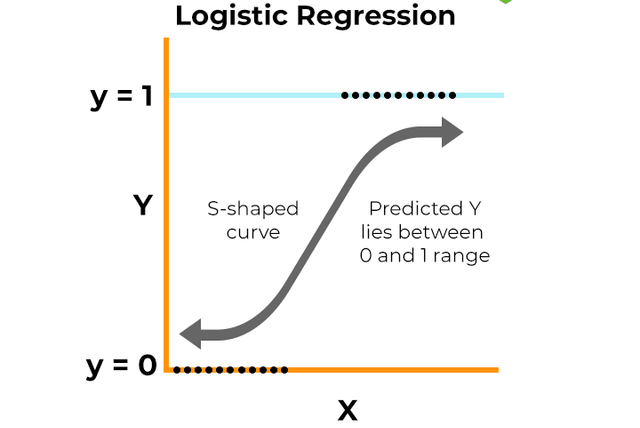
이는 곧, 확률에 대한 예측이므로 $P (y = 1∣ x)$ 이라는 conditional probability function(혹은 Bayes' Theorem에 따른 Posterior)이기도 하다.

Sigmoid function

$y = \frac{1}{1 + e ^{- (W^{⊤} x + b)}}$

$W^{⊤}$ 는 그래프의 경사도를 결정한다.
b는 그래프의 좌우 이동을 결정한다.

이를 통해, 0부터 1사이의 값으로 mapping 시킨다.
$W^{⊤} x$ 는 Linear classifier이 되며, 곧 decision boundary가 되는 hyperplane을 만들어주는 역할을 하게 된다. 그 경계가 되는 지점은, threshold에 의해 결정된다.

Exact Boundary

정확히는,

\frac{P ( Y = 0∣ X )}{P ( Y = 1∣ X )} = 1

을 만족할 때가 그 경계가 된다. class $0$ 인지 혹은 class $1$ 인지의 확률이 같아지는 지점을 말한다.

Probability function using MLE

Posterior를 최대화하기 위한 함수이므로, 결국은 MLE로 이어지는 함수가 되기도 한다.

$P (y = 1∣ x) = \frac{P ( x ∣ y = 1 ) P ( y = 1 )}{P ( x )} = \frac{P ( x ∣ y = 1 ) P ( y = 1 )}{P ( x ∣ y = 0 ) P ( y = 0 ) + P ( x ∣ y = 1 ) P ( y = 1 )}$
$= \frac{1}{1 + \frac{P ( x ∣ y = 0 ) P ( y = 0 )}{P ( x ∣ y = 1 ) P ( y = 1 )}}$

이 때, IID라는 가정이 존재한다고 하면,

\frac{P ( x ∣ y = 0 ) P ( y = 0 )}{P ( x ∣ y = 1 ) P ( y = 1 )} = \frac{P ( y = 0 )}{P ( y = 1 )} i = 1 \prod n \frac{P ( x _{i} ∣ y = 0 )}{P ( x _{i} ∣ y = 1 )}

에서, $\frac{P ( x _{i} ∣ y = 0 )}{P ( x _{i} ∣ y = 1 )} = exp (- w_{i} x_{i}), \frac{P ( y = 0 )}{P ( y = 1 )} = exp (- w_{0})$ 의 꼴로 변형된다고 생각하면(Gaussian Distribution을 취하는 것으로, 결국에는 Parametric Methods의 일종으로써 그 분포를 정해놓고 estimate하는 것이다), 결국은 Sigmoid꼴로 변하게 된다.

Multinomial Logistic Regression

$f (X; W) = X^{⊤} W + b$

$\frac{P ( Y = 1∣ X )}{P ( Y = K ∣ X )} = exp (X^{⊤} W^{1} + b^{1})$
$\frac{P ( Y = 2∣ X )}{P ( Y = K ∣ X )} = exp (X^{⊤} W^{2} + b^{2})$
$\frac{P ( Y = K - 1∣ X )}{P ( Y = K ∣ X )} = exp (X^{⊤} W^{K - 1} + b^{K - 1})$
$i \sum P (Y = i ∣ X) = 1$

위의 K개의 식들을 연립하면,

P (Y = i ∣ X) = \frac{exp ( X ^{⊤} W ^{i} + b ^{i} )}{j = 1 \sum K exp ( X ^{⊤} W ^{j} + b ^{j} )}

곧, Softmax의 형태의 꼴로 바뀌게 된다. 결국에는 MLE를 취한다고 하면, 이에 softmax에 log를 취해 그 값을 최소화하는, Softmax Loss에 대한 MLE로 변하게 된다.

즉, Logistic Regression은 softmax의 응용이다.